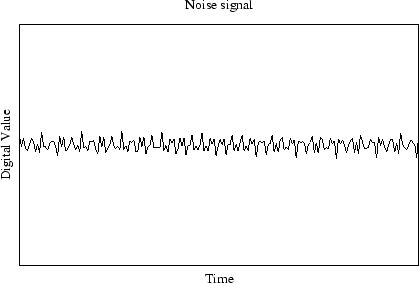
Fourier analysis breaks a vector of data apart into its individual basis functions. Any discrete signal can be completely represented by a sum of cosine functions of increasing frequency. In Fourier analysis, the strengths of the individual frequencies give strong evidences of the presence (or absence) of subsignals in the overall signal. Removal of noise from an audio signal, requires a digitial signature of the noise. The easiest way to get that signature is by sampling a "silent" portion of the audio track, i.e. the space between tracks on a vinyl LP. A noise sample may look like this:

If we add that noise signal to our example signal from the introduction, we get:

Now, if we subtract the noise signal from this we get our original signal back:
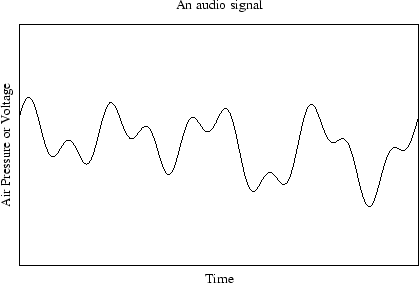
If the noise esimate and the actual noise imposed on the signal are identical, this works quite well. In practice, the noise signal doesn't change very much, and a single noise signature estimate can be used to clean up 20 minutes of audio.