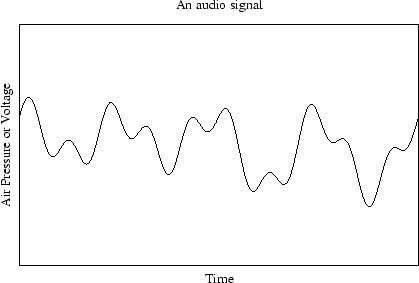
Audio signals are continuous, like this:

Digitizing the signal, means we loose some information as we sample at uniform time intervals, (44100 times per second for CD quality audio. Which means loss of information in the signal, the signal above digitized could end up looking like this:
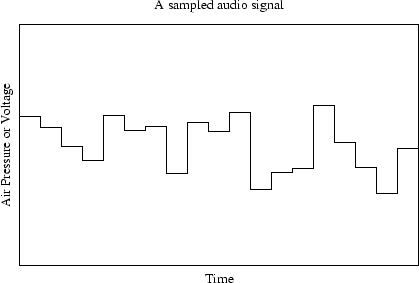
While this may look awful, we (humans) are make the problem simpler because the highest frequency we can perceive is about 20khz. Sampling at 44.1khz means the highest frequency we can represent is 22khz - so this represents no real loss in human-audio information.
The second issue is how to represent the magnitude of the signal. Using 1 byte gives us +/- 128 discrete values, using 2 bytes gives us +/- 32767 values. 2 bytes is the standard for CD audio and is sufficient for humans. There are applications for resolutions > 2 bytes, but that is really in the recording and mixing realms.
So, how much data is that, for 1 minute of CD audio?
2 channels X 44100 samples per second X 60 seconds * 2 bytes per sample = 10.5 Megabytes per minute. Get a large hard drive and a fast PC (or efficient OS like Unix for a slower PC :-)